图形推理之玩转四面体
在公务员的行测考试中,图推一直是同学们最为头疼的模块之一,而空间重构类的题目一直都是图形推理中比较难的部分,尤其是对于空间想象力较弱的同学来说,直接凭想象力很难准确的选中答案,但其实关于空间重构类的题目有很多的解题技巧可以帮助同学们,让大家免于空间想象力弱的困扰,今天我们就来看看对于四面体类的题目有怎样解题方法。
关于四面体的题目,一般情况下有两种考查形式。一种是折四面体类的题目,另外一种是拆四面体类的题目,如下图所示:
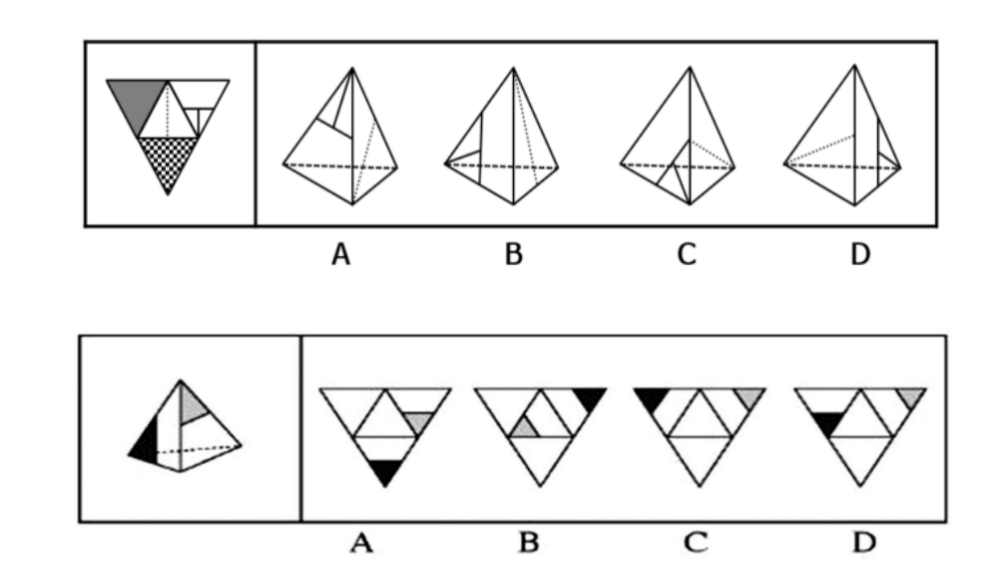
从上面这样两道题目我们可以发现,题目中出现的四面体都是正四面体,是由四个全等正三角形围成的空间封闭图形。那它有怎样的特征呢?我们先来认识一下四面体的结构:
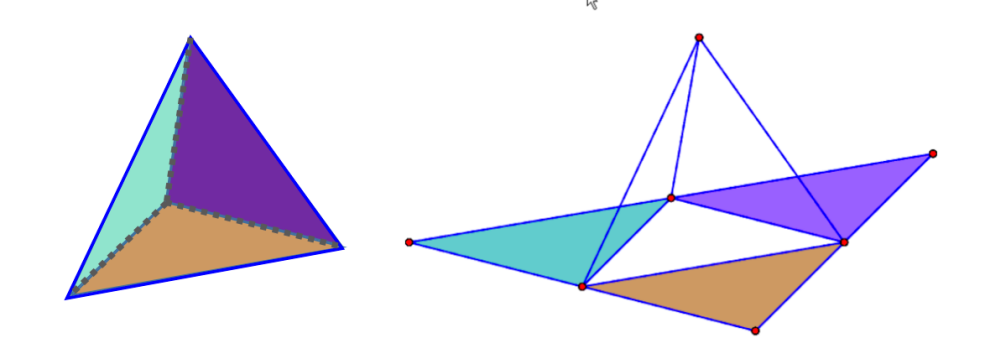
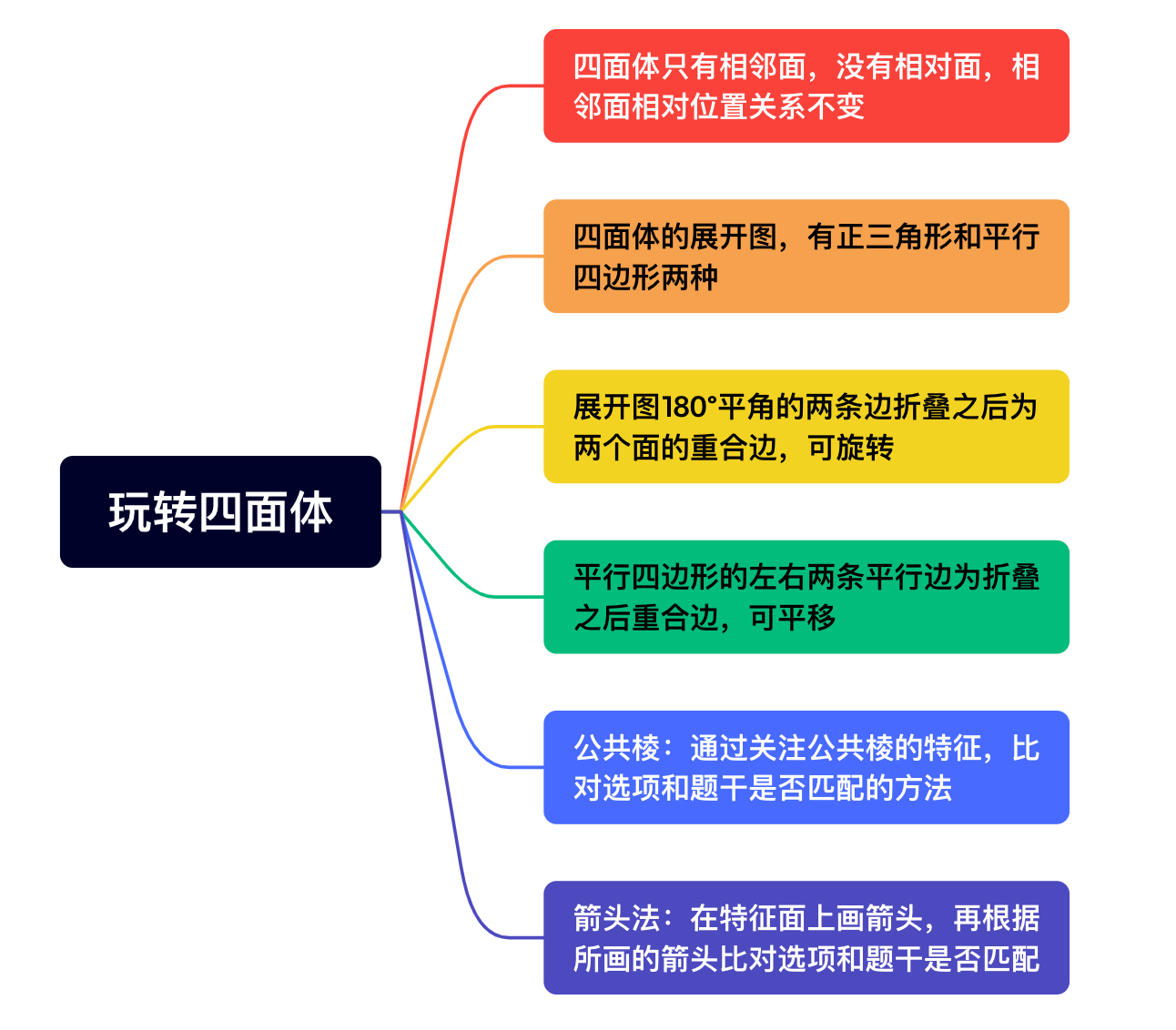
如上图所示,正四面体有4个面,6条棱,4个顶点,它们之间没有相对面。相比于六面体来说,四面体要相对好做很多,因为四面体只有相邻面,没有相对面,所以也就不存在寻找相对面,这里我们只需要清楚的知道四面体同样也存在着相邻面相对位置关系不变的准则。
我们将它的立体图展开,一般会形成下面两种展开图:
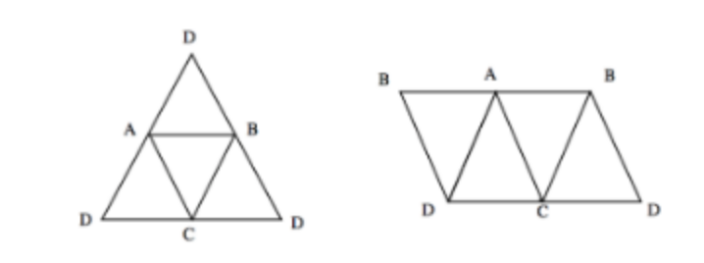
正四面体的展开图,有正三角形和平行四边形两种。在正三角形展开图中,DA与AD,DC与CD,DB与BD是公共棱,在平行四边形的展开图中,BA与AB,DC与CD,BD与BD是公共棱,由此我们得出两个非常重要的结论:
1、180°平角的两条边折叠之后为两个面的重合边,可旋转;
2、平行四边形的左右两条平行边为折叠之后重合边,可平移。
通过这两条结论,可以让我们很快的找到正四面体的公共棱,而公共棱法也是我们解四面体类题目中,最简单的一种方法。所谓的公共棱法就是通过关注公共棱的特征,比对选项和题干是否匹配的方法,具体我们看一下例题1。
例1:左边给定的是纸盒外表面的展开图,右边哪一项能由它折叠而成?请把它找出来:
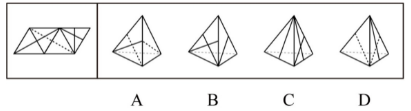
我们将例题1的平面展开图进行编号,分析选项:
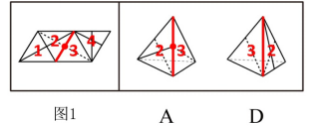
A项:面2和面3公共棱中点引出一条虚线和一条实线,而题干中引出两条虚线,排除;
D项:面2和面3的两条虚线不相交于公共棱中点,而题干中相交于公共棱中点,排除;
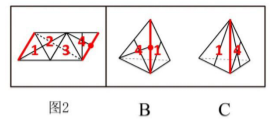
B项:面1与面4的公共棱中点引出一条实线,题干中此公共棱中点也只引出一条实线,暂时保留;
C项:面1与面4的公共棱中点没有引出线条,而题干中此公共棱中点引出一条实线,排除。
因此,这道题的正确答案是B选项。
除了我们常用的公共棱法,四面体的题我们还可以使用箭头法进行解题。采用箭头法时,我们可以先定位特征面(特征面的选取尽量要选择非中心对称的图形),然后在特征面上画箭头,再根据所画的箭头比对选项和题干是否匹配。
我们拿例题2来详细讲解一下箭头法。
例2:左边是四面体的展开图,下列哪项不能由此折叠而成?
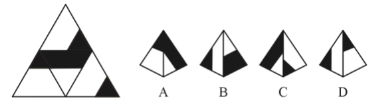
首先我们对题目中的图形进行编号,并选取特征面画箭头,如下图所示:
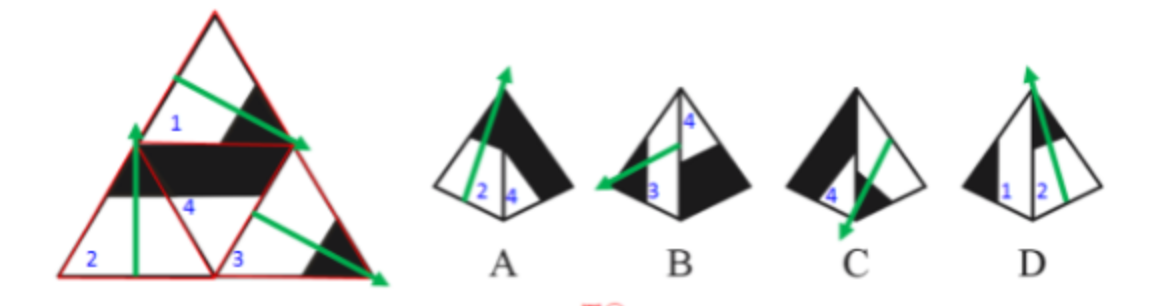
A项:该项出现一个黑三角面、4面,当黑三角面为2面时,两面位置关系与题干一致,可以折叠而成;
B项:该项出现一个黑三角面、4面,当黑三角面为3面时,两面位置关系与题干一致,可以折叠而成;
C项:该项出现一个黑三角面、4面,黑三角面为1面、2面、3面中任一面,两面位置关系均与题干不一致,无法折叠而成;
D项:该项出现两个黑三角面,当黑三角面为1面、2面时,如图②所示,两面位置关系与题干一致,可以折叠折叠而成。
因为题干中选择的是不能由此折叠而成的选项,所以例题2的正确答案是C。
公共棱法和箭头法是我们在解四面体时最常用的方法,相信同学们学会以后在应对四面体的题目时一定可以更准确的选出答案。
本文链接:https://ah.huatu.com/2024/0926/2934034.html
——相关阅读——
以上是2025国考备考:图形推理之玩转四面体的全部内容,更多资讯请继续查看:安徽人事考试网、国家公务员考试网。
——相关阅读——
(编辑:娜)

