安徽事业单位招聘网同步安徽华图发布职业能力测验：2022安徽事业单位备考：数量关系-数学运算-工程问题-效率类10题。更多关于安徽事业单位备考,2022安徽事业单位备考,事业单位备考的相关资讯，请关注安徽事业单位招聘网/安徽事业单位公众号和交流群
。
1. 村里修一段公路，计划20人修20天完工。开工5天后，有5人离开村子外出打工，剩下的15人继续修路。又过了10天后，再抽出5人去筹集资金。最后5天，筹集资金的有2人回来一起修路，如果每人工作效率一样，那么修完这段公路一共需要多少天?
A.25
B.29
C.30
D.32
【答案】B
【解析】
第一步，本题考查工程问题，属于效率类。
第二步，赋每个工人的效率为1，则修公路的工作总量为20×20=400，从抽出人去筹集资金到有2人回来这段时间为x天，根据题意可列式400=20×5+15×10+10x+(10+2)×5，解得x=9(天)，故修完公路共需5+10+9+5=29(天)。
因此，选择B选项。
2. 一项工作，甲、乙合作20小时可以完成，已知甲与乙的效率比为5∶4，则甲单独完成这项工作需要()小时完成。
A.46
B.40
C.39
D.36
【答案】D
【解析】
第一步，本题考查工程问题，属于效率类，用赋值法解题。
第二步，由甲与乙的效率比为5∶4，赋值甲的效率为5，乙的效率为4。则可求出工作总量为20×(5+4)=180，则甲单独完成这项工作所需时间为180÷5=36(小时)。
因此，选择D选项。
3. 有一件工作，丙单独做需10小时完成，乙、丙合作需4小时完成。甲2小时完成的工作量，乙需要3小时才能完成。现在这项工作由丙独做，他从清晨5时开工，必须在中午12时完工。甲、乙二人应帮助丙工作多少时间才能使丙准时完成工作?
A.4/5小时
B.1小时
C.4/3小时
D.2小时
【答案】A
【解析】
第一步，本题考查工程问题，属于效率类。
第二步，甲2小时的工作量与乙3小时的工作量相同，说明甲乙的效率之比3∶2，赋值甲的效率为9，乙的效率为6。同一项工作，丙一人10小时，乙丙4小时完成，说明乙4小时的工作量与丙6小时的工作量相同，则丙的效率为4，可求得总工作量为10×4=40。现在丙需要工作7小时，此时丙能完成的工作量为7×4=28，剩余12，需要甲、乙帮助丙工作12÷15=4/5(小时)。
因此，选择A选项。
4. 某公司接到一项任务，如果由甲乙两团队合作需要10个小时完成，如果由乙丙两团队合作需要12小时完成。如果先由甲丙两团队合作4小时，乙再单独去完成剩下的任务需要12小时，则这项任务全部由乙团队单独负责，需要()个小时完成。
A.12
B.15
C.16
D.18
【答案】B
【解析】
第一步，本题考查工程问题，属于效率类，用赋值法解题。
第二步，根据题意，按照工作总量一定，可得：10(甲+乙)=12(乙+丙)=4(甲+丙)+12乙，化简得：甲=2丙，乙=4丙，故赋值丙的效率为1，则甲的效率为2，乙的效率为4，工作总量为10×(2+4)=60。若乙团队单独负责，需要用时60÷4=15(小时)。
因此，选择B选项。
5. 完成项目A，甲乙丙单独完成的效率比为4∶5∶6。乙单独完成项目A的1/5后，甲丙合作4天完成整个工程。则共需要()天完成项目A。
A.6
B.7
C.5
D.8
【答案】A
【解析】
第一步，本题考查工程问题，属于效率类，用赋值法解题。
第二步，根据“甲乙丙单独完成的效率比为4∶5∶6”可赋值甲乙丙的效率分别为4、5、6。设工程总量为60x，则根据题意可列方程：60x(1-1/5)=4×(4+6)，解得x=5/6，则60x=50。
第三步，乙单独完成项目A的1/5所需时间为50×1/5÷5=2(天)，则共需要2+4=6(天)完成项目A。
因此，选择A选项。
6. 甲、乙、丙三个施工队共同完成一项工程需要6天时间，如果甲与乙的效率之比为4∶3，乙与丙的效率之比为2∶1，则乙单独完成这项工程需要()天。
A.12
B.17
C.24
D.32
【答案】B
【解析】
第一步，本题考查工程问题，属于效率类，用赋值法解题。
第二步，已知“甲与乙的效率之比为4∶3，乙与丙的效率之比为2∶1”，可根据倍数特性赋值乙的效率为6，则甲的效率为8，丙的效率为3。根据“共同完成一项工程需要6天时间”，可知工作总量为(8+6+3)×6=102。
第三步，则乙单独完成这项工程需要102÷6=17(天)。
因此，选择B选项。
7. 一项工程由甲乙两个工程队共同承担。若甲队先干5天，余下的工程乙队单独完成需要8天，共需花费98万元;若乙队先干4天，余下的工程甲队单独完成需要10天，共需花费94万元。假设甲乙两队每天所需花费都是固定值，那么由乙队单独完成这一工程需花费()万元。
A.86
B.90
C.102
D.110
【答案】C
【解析】
第一步，本题考查工程问题，属于效率类，用方程法解题。
第二步，设甲的效率为x，乙的效率为y，根据工程总量不变，列方程5x+8y=4y+10x，化简得5x=4y，赋值x=4、y=5。则工程总量为5x+8y=60，故乙单独完成需要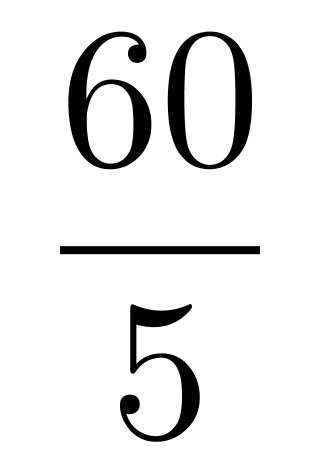
=12(天)。
第三步，设甲的费用为a万元，乙的费用为b万元，根据两次花费，可得5a+8b=98，4b+10a=94，解得a=6(万元)，b=8.5(万元)，所以乙单独完成需要的费用为12×8.5=102(万元)。
因此，选择C选项。
8. 小王和小李一起录入信息，小王比小李晚一天开始工作，且两人同时结束。已知小王的速度是小李的1.2倍，小李工作了6天。问若小王一个人完成这项工作，需要多少天?
A.8天
B.10天
C.12天
D.14天
【答案】B
【解析】
第一步，本题考查工程问题，属于效率类，用赋值法解题。
第二步，赋值小李的效率为1，小王的效率为1.2，根据小李工作了6天，小王工作了5天，可得工作总量为：1×6+(6-1)×1.2=12，故小王一个人完成这项工作需要12÷1.2=10(天)。
因此，选择B选项。
9. 王明抄写一份报告，如果每分钟抄写30个字，则用若干小时可以抄完。当抄完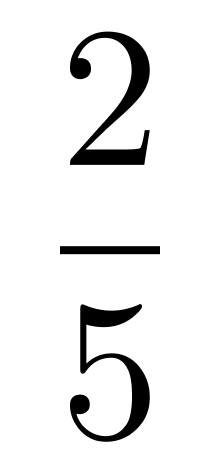
时，将工作效率提高40%，结果比原计划提前半小时完成。问这份报告共有多少字?
A.6025字
B.7200字
C.7250字
D.5250字
【答案】D
【解析】
解法一：
第一步，本题考查工程问题，属于效率类，用方程法解题。
第二步，设原效率完成剩余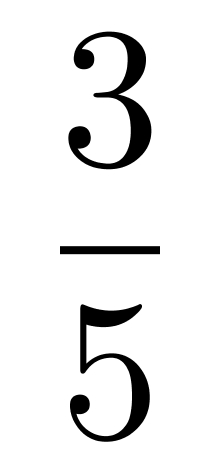
总量需要t分钟，则提高效率后需要(t-30)分钟。根据题意，列方程30t=(1+40%)×30×(t-30)，解得t=105(分钟)，则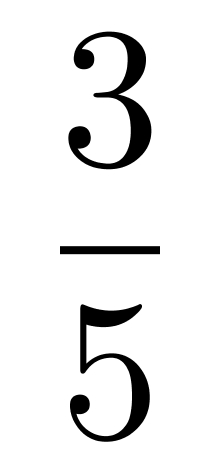总量=30×105=3150(字)，总量=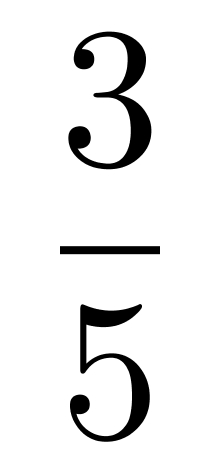×30×105=5250(字)。
因此，选择D选项。
解法二：
第一步，本题考查工程问题，属于效率类，用比例法解题。
第二步，“工作效率提高40%”，则提高后效率与原效率比为7∶5，工作总量相同时，工作时间比5∶7。提高效率后，时间比原计划提前了2份，2份=30分钟，故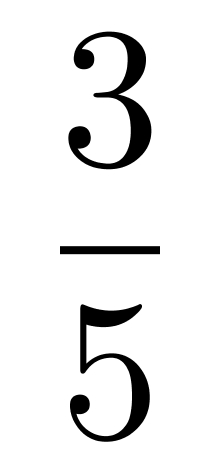的总量需要7×
=105(分钟)，总量=
×30×105=5250(字)。
因此，选择D选项。
10. 一项工程，A单位独立完成施工需要1年才能完成，A单位施工1个季度后B单位再施工2个月恰好完成工程的一半。现A、B两个单位合作一段时间后，剩下的部分由B单位单独完成，且两段时间相等，实际施工几个月?
A.4个月
B.7个半月
C.6个月
D.8个月
【答案】C
【解析】
第一步，本题考查工程问题，属于效率类，用赋值法解题。
第二步，设A、B单位的施工效率分别为x、y，根据题意可列式：12x=(3x+2y)×2，整理可得3x=2y，赋值A、B单位的施工效率分别为2、3，则工作总量为12x=24。
第三步，设A、B两个单位合作a个月，则B单位单独完成时间也是a个月。根据题意可列式：5a+3a=24，解得a=3(月)，则实际施工6个月。
因此，选择C选项。
本文链接：https://ah.huatu.com/2022/0301/2259780.html
——推荐阅读——
招聘公告--2022年安徽事业单位招聘公告|职位筛选|备考咨询
报名相关--2022安徽事业单位报名入口|报名统计|专业分类目录
辅导课程--2022年安徽事业单位笔试课程|面试课程|图书|网课
备考指导--2022安徽事业单位时政热点|每日一练| 资料|历年试题
以上是2022安徽事业单位备考：数量关系-数学运算-工程问题-效率类10题的全部内容，更多资讯请继续查看:安徽华图(https://ah.huatu.com/)、安徽事业单位招聘网(https://ah.huatu.com/sydw/)。
（编辑：sunmiaomiao）
