在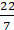 ,
,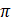 ,
,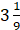 ,
,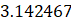 四个数中,最大的数是( )
四个数中,最大的数是( )
A. 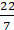
B. 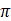
C. 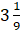
D. 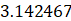
某几何体三视图如图所示,则该几何体体积是( )
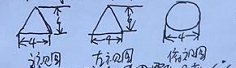
A. 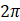
B. 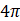
C. 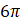
D. 
世界上大部分国家都使用摄氏温度,但有一些国家的天气预报仍然使用华氏温度,两种计量之间有如下对应:若两种计量之间的关系是一次函数,则100℃所对应的华氏温度为( )
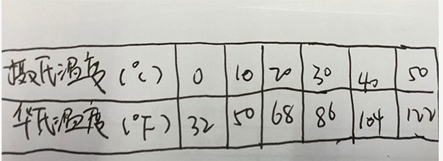
A.212
B.216
C.220
D.224
已知向量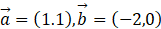 ,且向量→
,且向量→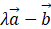 与
与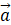 垂直,则实数
垂直,则实数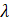 =( )
=( )
A.1
B. 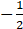
C.-1
D.-2
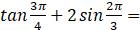 ( )
( )
A. 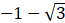
B. 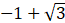
C. 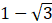
D. 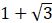
抛物线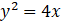 的焦点坐标是( )
的焦点坐标是( )
A. 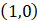 B.
B. 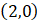 C.
C. 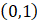 D.
D. 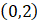
已知等比数列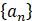 的公比为
的公比为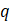 ,前
,前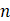 项和为
项和为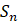 ,若
,若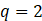 ,
,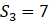 ,则
,则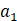 =( )
=( )
A.  B.1 C.2 D.3
B.1 C.2 D.3
正方体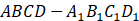 ,异面直线
,异面直线 与
与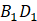 所成的角为( )
所成的角为( )
A.30° B.45° C.60° D.90°
如图,在直角梯形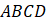 中,
中,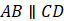 ,角
,角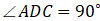 ,AC,BD相交于点E,过E点作EF垂直于DC,垂足为F,若AD=6,DF=4,则三角形BEC的面积为( )
,AC,BD相交于点E,过E点作EF垂直于DC,垂足为F,若AD=6,DF=4,则三角形BEC的面积为( )

A.6 B.12 C.24 D.36
关于“综合与实践”教学活动的实施,下列说法错误的是( )
A.教学实施以学生自主参与为主的学习活动,重在实践与综合。
B.教学内容是以问题为载体,选择恰当的问题是关键。
C.教学活动实施过程中教师的角色扮演是多重的。
D.教学活动评价强调过程性评价,不必关注结果性评价。
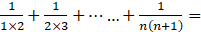 ___________
___________
曲线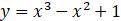 在点(1,1)处的切线方程为___________
在点(1,1)处的切线方程为___________
 ____________
____________
义务教育阶段“统计与概率”教学,其核心目标是帮助学生逐步建立_________观念,了解随机抽象。
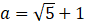 ,
,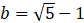 ,求
,求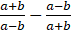 的值。
的值。
如图,直线AD,BC相交于点O,AD=BC,∠C=∠D=90°,若∠ABC=36°,求∠OAC的度数。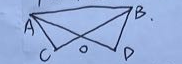
.已知甲乙两车速度比2:3,甲乙两车分别从A、B两地同时相对开出,在途中相遇后继续行驶,此时乙车提速三分之一,甲不变,当乙车到达A地时,甲车距B地还有24千米。AB两地距离为多少?
椭圆C: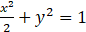 ,直线L过C的左焦点F和点M
,直线L过C的左焦点F和点M  ,且与椭圆交于A、B两点 (1)求直线L的方程 (2)求线段AB的长度
,且与椭圆交于A、B两点 (1)求直线L的方程 (2)求线段AB的长度
已知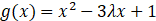 图像关于直线
图像关于直线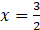 对称
对称
(1)求λ的值
(2)求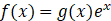 的单调区间
的单调区间
- 某教师执教小学教材比的应用一课,有这样一道习题的教学 长方形周长40cm 长与宽的比是3:2 求长方形的面积 全班同学出现如下两种方法:
方法一: 方法二:
3+2=5 3+2=5
40÷2=20(cm) 40÷5=8(cm)
20÷5=4(cm) 8×3=24(cm)
4×3=12(cm) 8×2=16(cm)
4×2=8(cm) 24÷2=12(cm)
12×8=96(平方厘米) 16÷2=8(cm)
12×8=96(平方厘米)
- 分析两种解法的理由
- 一些学生对方法2不理解思路,教学中应如何解决
数学探究是新课程标准倡导的基本观念之一,阅读并回答问题。
材料,某初中教材中,三角形全等的判定的部分内容。
我们知道,如果△ABC≌△A'B'C',那么它们的对应边相等,对应角相等。反过来如果△ABC与△A'B'C'满足三条边对应相等,三个角对应相等,即,AB =A'B', BC = B'C', AC = A'C', ∠A=∠A', ∠B=∠B', ∠C=∠C'
符合条件,就能保证△ABC≌△A'B'C'
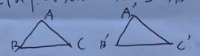
如果△ABC与△A'B'C'满足上述六个条件的一部分,那么能否保证△ABC与△A'B'C'全等呢?
探究1:任意画出一个△ABC,再画一个△A'B'C'使△ABC与△A'B'C'满足上述六个条件中的一个或两个,你画出的△ABC与△A'B'C'一定全等吗?
通过画图可以发现,满足上述六个条件中的一个或2个,△ABC与△A'B'C'不一定全等,满足上述六个条件中的三个,能保证△ABC与△A'B'C'全等吗?我们分情况讨论
探究2:任意画出一个△ABC,再画一个△A'B'C',使AB =A'B',BC = B'C', AC = A'C',,把画好的△A'B'C',放到△ABC上,它们重叠吗?
画出一个△A'B'C',使AB =A'B',BC = B'C', AC = A'C', 1.画线段BC = B'C', 2.分别以B’,C’为圆心,线段AB,AC为半径画弧,弧交于点A’, 3.连接线段A'B',A'C'
上图画△A'B'C'的方法,你是这样画的吗?探究2的反映了什么?由探究2可以得到判定两个三角形全等的一个方法:三边对应相等的两个三角形全等
用上述的结论可以判断两个三角形全等,判断两个三角形全等的推理过程叫做证明三角形全等
(1)教材编写意图和特点是什么?
(2)教材内容所蕴含的主要教学思想方法是什么?
(3)你认为数学探究教学有哪些基本教学观念?


