2022国家公务员考试行测试题答案解析(省部级):数量关系

2021-11-11 11:40 来源：安徽华图

　　国家公务员考试网同步安徽华图考试动态信息：2022国家公务员考试行测试题答案解析(省部级):数量关系。更多关于国家公务员考试,行测,国家公务员试题解析,安徽华图的信息的内容，请关注国家公务员考试网，以及安徽华图教育(anhuihuatu)认证号和交流群（）获取更多招考信息和备考资料。

2022国家公务员考试行测试题答案解析(省部级):数量关系

　　61. 某企业职工筹款给甲村学龄儿童购买学习用具，如按100元/人的标准执行则资金剩余550元，如按120 元/人的标准执行则还需筹集630元。现额外筹集2510元，且最终按80元/人的标准，正好能给甲、乙两村的学龄儿童购买学习用具。问乙村学龄儿童有多少人？

　　A.50

　　B.53

　　C.56

　　D.59

　　【答案】 B

　　【解析】

　　第一步，本题考查基础应用题。

　　第二步，设甲村学龄儿童x人，列方程100x+550=120x-630，解得x=59，现有资金100×59+550=6450元，

　　额外筹集后共有6450+2510=8960元，按每人80元的标准，可分给8960÷80=112人，乙村学龄儿童有 112-59=53人。

　　因此，选择B选项。

　　62. 甲、乙、丙、丁、戊5名职工参加党史知识测验，每人得分均不相同。甲和乙的平均分比丙多2分，丁和戊的平均分比丁多5分，甲、乙的平均分比丙、丁、戊的平均分多3分。问丙、丁、戊三人得分的排序为：

　　A.丙＞丁＞戊

　　B.丙＞戊＞丁

　　C.丁＞丙＞戊

　　D.戊＞丙＞丁

　　【答案】 D

　　【解析】

　　第一步，本题考查不等式问题。

　　第二步，根据题意可列三个方程， (①)， (②)， (③) ，通过方程②变形可得：戊-丁=10，那么戊＞丁，排除A 、C选项。方程③-①有，又丁=戊- 10，代入前面式子可得戊-丙=3.5，即戊＞丙，排除B选项。

　　因此，选择D选项。

　　63. 企业列出500万元设备采购预算，如用于购买x台进口设备，最后剩余20万元。经董事会研究后，决定购买质量更高的同类国产设备，单价仅为进口设备的75%。当前预算可购买x+3台，最后剩余5万元。问国产设备的单价在以下哪个范围内？

　　A.不到30万元/台

　　B.30—40万元/台之间

　　C.40—50万元/台之间

　　D.50万元/台以上

　　【答案】 C

　　【解析】

　　第一步，本题考查基础应用题。

　　第二步，买进口设备花费480万元，买国产设备花费495万元。设能买进口设备x台，那么买国产设备(x ＋3)台。根据国产设备单价为进口设备单价的75%可列方程： 480÷x×75%＝495÷ (x＋3)，解得x＝8，

　　那么能买国产设备11台，单价为495÷11＝45 (万元)。

　　因此，选择C选项。

　　64. 甲和乙两个乡村图书室共有5000本藏书，其中甲图书室的藏书比乙图书室多3x本，现从甲图书室中取出150本书放入乙图书室后，甲图书室的藏书仍比乙图书室多2x本，问甲图书室原有图书多少本？

　　A.2500

　　B.2750

　　C.2950

　　D.3500

　　【答案】 C

　　【解析】

　　第一步，本题考查基础应用题。

　　第二步，设乙图书室原有藏书N本，那么甲图书室本数为N+3x，取出150本后比乙多N+3x－ 150－(N+150) =3x-300，由题意3x－300=2x，解得x=300。那么甲图书室原有藏书(5000－300×3) ÷2+300×3=2950 (本)。

　　因此，选择C选项。

　　65. 李某骑车从甲地出发前往乙地，出发时的速度为15千米/小时，此后均匀加速，骑行25%的路程后速度达到21千米/小时。剩余路段保持此速度骑行，总路程前半段比后半段多用时3分钟。问甲、乙两地之间的距离在以下哪个范围内？

　　A.不到23千米

　　B.在23—24千米之间

　　C.在24—25千米之间

　　D.超过25千米

　　【答案】 D

　　【解析】

　　第一步，本题考查行程问题。
　　第二步，总路程前半段比后半段多用时3分钟，根据后的路程为匀速运动，可知总路程的前，比最后多用时3分钟。根据前路程为匀加速运动可知平均速度为=18千米/小时，设前路程用时为t小时，则最后路程用时为t－小时，列方程18t=21 (t－)，解得t=，则前路程为18×=6.3

　　千米，全程为6.3×4=25.2千米。

　　因此，选择D选项。

　　66. 高校某专业70多名毕业生中，有96%在毕业后去西部省区支援国家建设。其中去偏远中小学支教的毕业生占该专业毕业生总数的20%，比任职大学生村官的毕业生少2人，比在西部地区参军入伍的毕业生多1 人，其余的毕业生选择去国有企业西部边远岗位工作。问去国有企业西部边远岗位工作的毕业生有多少人？

　　A.32

　　B.29

　　C.26

　　D.23

　　【答案】 C

　　【解析】

　　第一步，本题考查基础应用题。

　　第二步， 70多名毕业生中，在毕业后去西部省区支援国家建设有96%，即24/25，说明毕业生总数是25的倍数，即75人，毕业后去西部省区支援国家建设的有72人，去偏远中小学支教的毕业生占该专业毕业生总数的20%，即75×20%=15人，任职大学生村官的毕业生=15+2=17，西部地区参军入伍的毕业生=15-1=14，所以去国有企业西部边远岗位工作的毕业生=72- 15- 17- 14=26。

　　因此，选择C选项。

　　67. 某地引进新的杂交水稻品种，今年每亩稻谷产量比上年增加了20%，且由于口感改善，每斤稻谷的售价从1.5元提升到1.65元。以此计算，今年每亩稻谷的销售收入比上年高660元。问今年的稻谷亩产是多少斤？

　　A.2200

　　B. 1980

　　C. 1650

　　D. 1375

　　【答案】 C

　　【解析】

　　第一步，本题考查基础应用题。

　　第二步，设去年稻谷亩产量为5x斤，则今年亩产量为6x斤，根据销售收入比上年高660元列方程， 1.65×6x- 1.5×5x=660，解得x=275，今年的稻谷亩产是6x=1650斤。

　　因此，选择C选项。

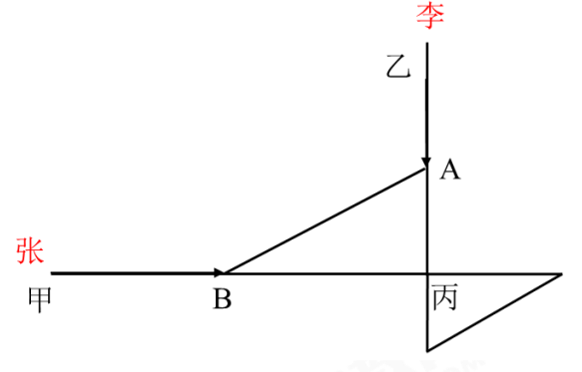
　　68. 甲地在丙地正西17千米，乙地在丙地正北8千米。张从甲地、李从乙地同时出发，分别向正东和正南方向匀速行走。两人速度均为整数千米/小时，且1小时后两人的直线距离为13千米，又经过3小时后两人

　　均经过了丙地且直线距离为5千米。已知李的速度是张的60%，则张经过丙地的时间比李： A.早不到10分钟

　　B.早10分钟以上

C.晚不到10分钟

　　D.晚10分钟以上

　　【答案】 D

　　【解析】

　　第一步，本题考查基本行程类。

　　第二步，已知李的速度是张的60%，可设张的速度为5v千米/小时，李的速度为3v千米/小时，两人1个小时的路程分别为5v千米、 3v千米，进而可得A点到丙地的距离为(8-3v) 千米，B点到丙地的距离为(17-5v) 千米，又已知AB=13千米，根据常用勾股数(5,12,13) 不难判断8-3v=5 ，17-5v=12，可得v=1千米/小时，那么张和李的速度分别为5千米/小时和3千米/小时，张从出发到丙地共用时17÷5=3.4小时=3小时24分钟，李从出发到丙地共用时8÷3×60=160分钟=2小时40分钟，张经过丙地的时间比李要晚44分钟。

　　因此，选择D选项。

　　69. 某县通过发展旅游业来实现乡村振兴，引进了甲、乙、丙、丁、戊和己6名专家。其中甲、乙、丙是环境保护专家，丁、戊、己是旅游行业专家，甲、丁、戊熟悉社交媒体宣传。现要将6名专家平均分成2 个小组，每个小组都要有环境保护专家、旅游行业专家和熟悉社交媒体宣传的人，问有多少种不同的分组方式？

　　A. 12

　　B.24

　　C.4

　　D.8

　　【答案】 D

　　【解析】

　　第一步，本题考查排列组合问题。

　　第二步，解法一：因只分为2组，可使用枚举法。根据题目要求有(甲乙丁，丙戊己)、(甲乙戊，丙丁己) 、(甲乙己，丙丁戊) 、(甲丙丁，乙戊己) 、(甲丙戊，乙丁己) 、(甲丙己，乙丁戊) 、(甲丁己、乙丙戊)、(甲戊己、乙丙丁)共8种分组方式。

　　因此，选择D选项。

　　解法二：本题可使用平均分组模型进行求解。将6名专家平均分成2组，每组3人，有种分组方式，

　　但是要从其中排除掉不符合题意的2种情况，分别是 (甲乙丙，丁戊己) 和(甲丁戊，乙丙己) ，有10-2=8 种分组方式。

　　因此，选择D选项。

　　70. 某水果种植特色镇创办水果加工厂，从去年年初开始通过电商平台销售桃汁、橙汁两种产品。从去年 2月开始，每个月桃汁的销量都比上个月多5000盒，橙汁的销量都比上个月多2000盒。已知去年第一季度桃汁的总销量比橙汁少4.5万盒，则去年桃汁的销量比橙汁：

　　A.多不到5万盒

　　B.少不到5万盒

　　C.多5万盒以上

　　D.少5万盒以上

　　【答案】 B

　　【解析】

　　第一步，本题考查数列问题。

　　第二步，设去年第一个月的桃汁销量为x万瓶，橙汁销量为y万瓶。桃汁、橙汁的每月销量都成等差数列，则第一个季度桃汁的销量为(x+0.5) ×3，橙汁的销量为(y+0.2) ×3，由题意(y+0.2) ×3－(x+0.5) ×3=4.5，有y－x=1.8。根据等差数列求和公式，全年桃汁总销量为[x+ (x+0.5×11) ]×12÷2=6 (2x+5.5)；橙汁总销量为[x+ (x+0.2×11) ]×12÷2=6 (2y+2.2)，两者之差为12 (x－y) +33－ 13.2=－ 1.8 (万盒)。桃汁比橙汁少不到5万盒。

　　因此，选择B选项。

　　71. 救灾部门紧急运送两批大米分给受灾群众，已知甲村人数是丙村的2倍，如果买两批大米都给甲村，每人正好能分24斤；如果第一批大米分给乙村，每人正好能分12斤，第二批大米分给甲、乙、丙三个村，每人正好能分4斤。为尽量保障受灾群众的基本需求，现决定另运送一批面粉分给甲村，并将两批大米都分给乙、丙两村，问乙、丙两村平均每人分到的大米重量在以下哪个范围内？

　　A.不到14斤

　　B. 14— 15斤之间

　　C. 15— 16斤之间

　　D. 16斤以上

　　【答案】 B

　　【解析】

　　第一步，本题考查基础应用题。

　　第二步，设丙村的人数为x，那么甲村的人数为2x，大米的总量为2x×24=48x。设乙村人数为y，则由题意 12y+4 (2x+y+x) =48x，化简为4y=9x，乙村人数为9x÷4=2.25x。大米平均分配给乙丙二村，每人可分48x÷ (2.25x+x) =192/13≈14.8 (斤)。

　　因此，选择B选项。

　　72. 为降低碳排放，企业对生产设备进行改造，改造后日产量下降了10%，但每件产品的能耗成本下降了50%，其他成本和出厂价不变的情况下每天的利润提高10%。已知单件利润=出厂价-能耗成本-其他成本，且改造前产品的出厂价是单件利润的3倍，则改造前能耗成本为其他成本的：

　　A.不到1/4

　　B. 1/4~1/3之间

　　C. 1/3~1/2之间

　　D.超过1/2

　　【答案】 B

　　【解析】

　　第一步，本题考查经济利润问题。

　　第二步，根据题干中的百分数进行赋值，赋值改造前的日产量、能耗成本分别为10和2，则改造后的日产量和能耗成本则为9和1。假设其他成本为x，单件利润为y，则出厂价为3y，改造前，y=3y-2-x，改造后利

　　润提高了10%，即9 (3y-1-x) =1. 1×10×y=1. 1×10× (3y-2-x) ，解方程可得x=7，y=4.5。改造前能耗成本与其他成本的比值为2/7≈28.6%，在B选项的范围内。

　　因此，选择B选项。

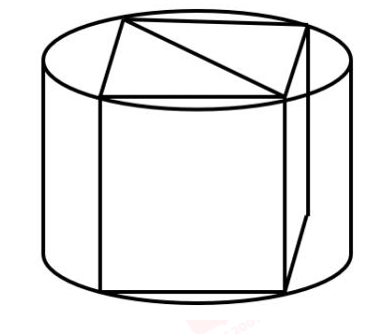
　　73. 一个圆柱体零件的高为1，其圆形底面上的内接正方形边长正好也为1。现将该圆柱体零件切割4次，得到棱长为1的正方体，则切去部分的总面积为：

　　【答案】 A

　　【解析】

　　第一步，本题考查几何问题，属于立体几何类。

　　第二步，如图所示，底面圆的内接正方形的面积为1，则边长为1，对角线长为，可知底面圆的半径为

。切割下去的四个部分总表面积相当于(一个圆柱的表面积－上下表面两个正方形) ＋立方体的侧面积，代入数据为=。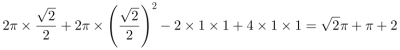

　　因此，选择A选项。

　　74. 甲和乙两条效率相同的生产线从早上不同时间开始生产同一种产品，到中午12：00时分别正好生产了 x件和y件。已知乙生产x件时，甲生产了54件；甲生产y件时，乙生产了1.5x件。如乙从9：00开始生产且12：00后两条生产线仍保持原有速度，问两条生产线生产的产品总量达到500件是在什么时候？

　　A. 16：30之前

　　B. 16：30 ~ 17：00之间

　　C. 17：00 ~ 17：30之间

　　D. 17：30之后

　　【答案】 D

　　【解析】

　　第一步，本题考查基础应用题。

　　第二步，两条生产线相率一样，根据两者生产件数差值不变可列方程组： y－x＝x－54＝ 1.5x－y，解得x＝72 ，y＝90，即9— 12点乙一共生产了90件，那么效率为，距离500件还差500－72－90＝338(件)，需要338÷60＞5.5 (小时) ，即17点30之后。